Abstraction and Generalization II: Mathematical Abstraction
This is part II or my attempt to create a methodology of abstracting and generalizing. As I said in the preamble. I kind of got confused. But here it is, with all of its defects. Comments are welcomed
This essay was supposed to be a simple explanation of why and how mathematical abstraction and generalization could be used as a model for using abstraction and generalization for decision making tools. I was driven by the milieus where I had experience: engineering problem solving, teaching engineering, and coaching sports. As it turned out, creating such a model sent me into a paroxysm of mental confusion because there were so many contradictions that bubble up to the surface. I am not sure if I have adequately addressed all the gaps and loopholes in reasoning on this subject, but as I had said: “I write to find out what I think,” so here is a microcosm of my thought process and reasoning. Please look upon it as a thought experiment that it is and feel free to communicate with me about any lapses in reasoning and logic and at the same time, I would like to construct a sturdy structure for this tool so that oversimplification and overgeneralization can be avoided.
In Abstractions and Generalizations I: Background and Thinking (https://thecuriouspolymath.substack.com/p/abstractions-and-generalizations), I explained why I wanted to research the human abilities to abstract and generalize: I wanted to take advantage of this natural human habit to abstract and generalize as a tool to help us make better decisions. We humans always subconsciously and automatically abstract common details from our perceptions, experiences, and existing knowledge to create narrative that we can understand. Indeed, in Alan Watts’ tome on Zen Buddhism The Way of Zen, (Watts, 1957), he describes abstraction as: “…a necessity for communication, which enables us to represent our experiences with simple and ready-made “grasps” of the mind.”
This habit is how we can aggregate experiences and knowledge to convert them into useful heuristics to apply when we make decisions. My intention is to explore how to better use our abstraction and generalization habits to make better decisions, even though the extemporaneous factor is lost.
Our abstraction and generalization habit, however, is performed with the subconscious System 1, as explained by Daniel Kahneman (Kahneman, 2013), as such, our proclivity is to over abstract and overgeneralize because the subconscious System 1 responds instantaneously, subconsciously, and without constraint because the conscious System 2 is not actively engaged to guide our abstraction and generalization. As a result, the unconstrained abstraction and generalization can vary erratically and come to erroneous conclusions.
Ironically, this subconscious habit of ignoring the facts and constraints while abstracting and generalizing is exactly what many believe inspires our creativity and ingenuity; the lack of constraints from System 2 liberates our creative urges from being overly risk-averse, which permits us to take greater risks and think more broadly when abstracting and generalizing, which injects serendipity into our thoughts. The downside of this cognitive emancipation is that many of the original and creative ideas that we generate are often infeasible, unrealistic, and not applicable. These ideas are mixed with feasible, realistic, and applicable solutions in a large mishmash of plausible solutions. To make them useful to our purposes, these solutions need to be vetted deliberately by consciously engaging System 2 to bring the solutions back to reality. We end up spending copious amounts of time sifting through the large amount of generated solutions to uncover the feasible solutions. The crux of the argument for using the constrained abstraction and generalization approach is to generate a smaller number of applicable solutions, to obtain pragmatic, less uncertain, lower reward, and lower risk results that could be applicable to the question and meets the stated purpose and contexts.
We have the luxury to choose to operate between the two extremes by iterating and selectively adjusting the levels of abstraction and generalization as guided by the potential solutions’ ability to meet the purpose. The constrained approach is reversing the thought process from the unconstrained approach; whereas the unconstrained approach generates a large number of imaginative solutions which need to be sorted; the constrained approach hews closer to the purpose and context and generates less, but more feasible, solutions.
Having a large number of plausible solutions in the solution space could be overwhelming as they all need to be vetted and filtered, whereas having a much smaller solution space allows us to better consider the nuances of the solutions and it is easier to loosen the constraints, which causes the bottleneck. Any solution that results from the tightly constrained approach are not the only possible solutions; if the tightly constrained approach results in no solutions because the constraints are too limiting, the constraints can be adjusted — loosened and tightened — to tune the solutions, the stated purposes can also be revisited to guide the exploration of possible solutions.
Another human factor that affects the fidelity of the solutions is outlined in Chapter 9 of Kahneman’s book (Kahneman, 2013), titled Answering an Easier Question, Kahneman describes our unconscious tendency to answer the questions that are easier to answer rather than the question that we set out to answer. The tendency is to accept solutions that results from unconstrained abstraction and generalization exercise which answers the easier question rather than the original desired question. The amount of unknown variables that accompanies the results from unconstrained abstraction and generalization — depending on the circumstances — could be complicating and will distract from the specified purpose and answer the easier questions just so we can make the decision making easier.
The two books by the mathematician Eugenia Cheng, (Cheng, How to Bake Pi: An Edible Exploration of the Mathematics , 2016) and (Cheng, The Joy of Abstraction: An Exploration of Math, Category Theory, and Life, 2022), qualitatively outlined the purpose and process of mathematics, and explained the methodology employed by mathematicians to create structures and procedures which allows them to be creative while also being strictly constrained so that the results are logical. Abstraction and generalization are two of the tools wielded by theoretical mathematicians to advance a field that exists primarily in the mind. The veracity of the mathematician’s conjectures must be verified by their fellow mathematicians through using rigorous proofs. The proofs are debated over by other mathematicians while using the same logic that the proposer used in their proofs, but the standard of proof is never debated. In other words, there is no such thing as close-enough, it is either proven, proven while being subjected to more constraints and modifications, or disproven by consensus. This kind of certainty in providing proof is welcome change from the wildly variable generalization humans use daily.
Another way to look at abstractions in mathematics is to see each abstraction as a separate facet of reality, each abstraction can be thought of as examining the specific reality from different points of view, a different context. The mathematician can accrue as many context-dependent perspectives on the specific real-life situation as possible to help the mathematicians gain understanding of the many perspectives on reality; indeed, reality can be interpreted and imagined as the summation of all the different facets. This point of view is akin to the parable of the eight blind men trying to describe an elephant as they are each examining just a single part of the elephant.
The direct question is: why choose abstraction and generalization practices of mathematics as the model for everyday decision making? Indeed, it seems to be an overkill to model decision making on something so specific as mathematics. There are several good reasons. This is probably a case of over constraining, but the good news about over constraining is that we are always at liberty to loosen the constraints.
As Cheng states: mathematics is an abstraction of real life; it is an idealization of the reality that we must live in; which is why reality is the inception point of the illustration. Indeed, life ( the reality) is quite different from mathematics (the idealization), mainly because:
· Life is real, mathematics is not real.
o Mathematics is the idealization of what is real, what we see, what we know, and what we perceive.
o Q: What can we do with our non-mathematical reality and idealize what is real, what we see, what we know, and what we perceive?
· Life is hard, mathematics is easy.
o This is because mathematics strictly follows logic, whereas life does not. Life is full of intuition, interpretation, leaps of faith, and uncertainties.
o Q: How can we replace mathematical logic with something that is not on the same level as mathematical logic, but serviceable?
· Life is not rational. Mathematics is always rational by definition.
o If mathematics turns out to be not rational, then it is not mathematics.
o Q: This is where our non-mathematical reality falls far short of mathematics, what if we can use our pre-determined purpose to rationalize and define our reduced and understandable perceptions of reality.
The natural question then is why do I want to try using mathematical abstraction and generalization as a model to help us alleviate our difficulties with reality? What can we accomplish with applying mathematical abstraction and generalization? What gap could be bridged?
· What makes reality difficult to understand is that we are human and do not deal well with the complexity of reality with our limited working memory. Our intuitions are not strong enough to adequately deal with realities.
o Mathematics helps humans construct and understand arguments that are too difficult for our intuition by reducing them and pruning away unnecessary details.
o Q: Can we use mathematical abstraction and generalization to understand arguments that are too difficult for our intuition by reducing them via applying a purpose, pruning away unnecessary details, and constructing a simpler and equivalent question?
· Humans struggle with ambiguity, and the realities of life are full of ambiguities.
o Mathematics is applied to eliminate ambiguities.
o Q: Can we use mathematical abstraction and generalization thinking in conjunction with specifically stated purposes to eliminate ambiguities?
· Reality is made up of many dimensions and details and humans don’t have the wherewithal to deal with all the dimensions and details in all their nuances.
o Mathematics cuts corners, answers questions by grouping similar questions together by showing that they are, in essence, the same questions.
o Q: Can we use mathematical abstraction and generalization thinking with specifically stated purposes to cut unnecessary corners, answers questions by grouping similar questions together by showing that they are, in essence, the same questions?
· Humans lose track of all the details when delving into granularities as our focus becomes narrow and we concentrate on the small picture.
o Mathematic abstractions take broad views, turning minute details into broad concepts.
o Q: Can we use mathematical abstraction and generalization thinking coupled with specifically stated purposes to take broader views, to turn minute details into broad concepts?
What follows is my interpretation of the mathematical abstraction and generalization process, as I gleaned the ideas from my readings of Cheng’s books. I take full responsibility for the errors in interpretation.
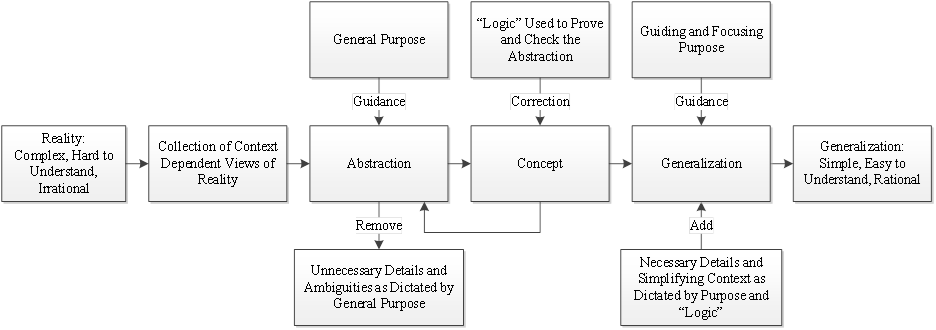
The figure below is how I envisioned the flow diagram of an application of the rigors of mathematical abstraction and generalization to general decision making. It is obviously not definitive; it is just a starting point for discussions.
Starting from the left side of the block diagram, we start with reality. It is complex, hard to understand, and irrational. The next box over is a collection of the reality as we perceive it. Our perceptions are dependent on context, which means that they represent different facets of reality. The word context designates specific factors to be accounted for in the snapshot of reality that is used for abstraction as well as for generalization.
Context is the circumstances of the situation being abstracted: such factors as the initial and boundary conditions constraining the situation, the time scales and time lags that are inherent in the situation, the central elements involved in the situation, and the total number of elements.
The next set of boxes : general purpose, abstraction, and the removal of details and ambiguities boxes make up the abstraction stage. The combined intent of all three is to:
· Strip away irrelevant details.
· Help us make connections between different contexts.
o Connections allow us to collect all the facets of the context examined and find common points.
· Helps us use the connections and draw analogies because we are cognitively predisposed to them.
o Analogies being the connections between the known and unknown.
o Analogies allow us to explore and create new and more abstract concepts.
o Analogies make us more comfortable with new abstract concepts because the new concepts are rooted in being analogous to known experiences and knowledge that we trust.
o Analogies also need to be specific and in detail.
The driving force for abstraction and generalization in mathematics is the purpose, as it will be for this exercise in analogizing the intended abstraction and generalization methodology to the mathematical abstraction and generalization methodology . The purpose defines the boundaries, whether the results are acceptable, whether the exercise should be reiterated with different constraints, and when the abstraction and generation should be stopped because the purpose has been met.
The purpose shows up in two boxes above both the abstraction and generalization boxes, it is the focal point of the argument supporting the process; the purpose is the key to creating the supporting structures and guard rails to prevent the process from unintentionally veering away unchecked because of feature creep or as our attention wanders. The definition of the purpose is critical for the abstraction stage; the purpose needs to be concisely and precisely defined and detailed to provide strict guardrails to prevent the tendency to depend strictly on intuition.
A note of caution, human intuitions are based on unverified and unverifiable beliefs, depending on just the intuition for abstraction can result in results that misleads. Although oftentimes we are forced to use intuition in case there is not enough information nor enough time to collect the information.
The general purpose is applied to the abstraction stage to keep the process from evolving into something that is not intended. The second purpose guides and focuses on the generalization stage so that the generalization result is channeled towards specific and detailed purposes.
A reminder that the methods and framework used to guide the abstractions are important, more important than the reality that we are abstracting from, the methods and frameworks should be flexible enough to pare away the unnecessary details while still retaining the components of reality that are necessary to meet the stated purpose. The bottom box in the abstraction stage are the tools that allow experimentation to happen; they are the details of reality that we choose to remove or retain so that the abstraction meets the purpose.
It is also important to experiment with the level of abstractions, playing with the contexts and the details, so that the right level of abstraction is selected to meet the purpose. This could be a highly iterative process, iterating between the abstraction and the Concept stage in the middle of the diagram.
Each experiment with the level of abstraction is:
· Not about right or wrong.
· Not about the absolute truth.
· About the chosen contexts and what makes them fit into the chosen purpose.\
· Results that are more abstract do not mean that they are less relevant, or even more difficult.
· The abstraction results need to fit the purpose.
In the end, the check list for the abstraction result must:
· Make sure the abstraction works as intended.
· Refine the abstractions so that they work as intended.
· Develop new theories from the abstractions.
The two boxes in the middle of the diagram are labeled “Concept” and “Logic.” These two boxes comprise the checking portion for the process. The concept stage is the result from the abstraction stage, after having been checked against the purpose and been stripped of the unnecessary details. The “clean” concept is then tested by the “Logic,” this is where it gets ambiguous and amorphous.
In mathematics, “Logic” is the ultimate measure of the concept; mathematical logic is applied to the concept to determine whether the concept can be proven true or false. This is how mathematicians decide whether the concept is correct according to mathematical logic, if it is, the concept is in the generalization stage, and can be generalized into a simple, easy to understand, and rational simplification of the complex, hard to understand, and irrational reality.
In mathematics, logic and abstraction are related:
· Logic builds rigorous arguments.
· Abstraction makes sure that the logic can be rigorous.
· Abstraction → Rigor → Logic → Math
There is nothing in the non-mathematical realms that serves the same role as “logic” in mathematics. There is nothing that can absolutely prove the truth of any hypothetical as “logic” does in mathematics. In the sciences, the hypotheses are checked and proven by empirical and experimental means; in engineering, the conjectures are checked by experimenting with prototypes, or more recently, with simulations — which is still somewhat controversial; but there is nothing which absolutely verifies any new ideas conceptually without empirical evidence. In the social sciences, empiricism is also the determiner of the veracity of any hypothesis or conjecture. Copious amounts of experiments are conducted with the requisite number of test subjects and examined closely with statistical tools to determine whether the hypothesis or conjectures are true or not. In those instances, it is possible to divide the “proof” into segments to preserve those parts that are “true” and those that are “false.” This is where the iteration between “concept” and “abstraction” naturally happens, and the idea of adjusting the levels of abstraction comes into play so that the concept passes the purpose and “logic” tests.
In this instance, the abstraction stage applies induction to the contextual views of reality and generates the “concept,” as the generalization stage takes the “concept” after having been proven by “logic” and applies deduction to generate ideas; ideas that needs to be verified by empirical investigations. The question then is: what should be the “logic” that we apply to the “concept” to ensure that the post generalization ideas are valid and are provable empirically?
In the STEM world, the existing paradigm governing the sciences can serve as the “logic” as well as the established physical laws, while the choice of applying the existing paradigm as the counterpart to “logic” is solid, the existing paradigm is always subject to “paradigm shifts”, which fits structure of the scientific revolutions that Thomas S. Kuhn outlined in his exploration of the scientific process, The Structure of Scientific Revolutions. (Kuhn, 1970). “Paradigm shifts” are the result of the adjustment or revision of paradigm to incorporate anomalies that consistently results from the empirical verification.
The existing paradigm can also be applied in the social sciences as the “logic,” but it results in more iterations and is dependent on variability of existing population studies, which makes it much more statistically dependent. It is certainly not as robust as being dependent on the physical laws, but the dependence on population studies is not a showstopper.
It became clear that the process needs to be iterative because of the choice of using existing paradigms in place of “logic”, which means that the abstraction and “concept” stages need to be iterated many times as the levels of abstractions are repeatedly adjusted to meet both the purpose and the “logic”. This is indeed how abstraction and generalization work in reality, numerous iterations are necessary as the levels of abstractions are adjusted and then attempted verification by empirical means.
Finally, the “concept,” after having been vetted by “logic” can be generalized, and the concepts can be deduced into broadly applicable ideas. The purpose of the results of generalization is to make a concept general by starting with a seed situation, modifying the situation to make it more applicable generally, creating rules that are due to the situations as imposed by the guiding and focusing purpose, and breaking rules to test the strengths and boundaries of the existing constraints and assumptions.
Some things to keep in mind while generalizing:
· The goal is to add dimensionality to ideas, not to make the generalization more real.
· Use generalization to relax conditions:
o To make the “concept” more flexible and variable, i.e., to incorporate as much of the necessary contexts as possible without veering astray.
o To not increase the coverage of the generalization.
o To turn the analogies from abstraction into real ideas
Experiments can be conducted by ignoring some outlying constraints temporarily to focus on the maximum population to see what results and then study both the central concept and the outliers together to see what results.
This proposed methodology is too pedantic and cumbersome for making instantaneous decisions, the process takes considerable amount of effort. The structure of the process needs to be tested before it can be streamlined. In other words, this idea for creating an abstraction and generalization needs to be abstracted and generalized by putting it into practice.
This is how the idea of using synthesis and analysis to test this process of abstraction and generalization came to mind. https://polymathtobe.blogspot.com/2023/07/volleyball-coaching-life-synthesis-and.html
Synthesis is defined in many ways:
· the composition or combination of parts or elements to form a whole.
· the combining of often diverse conceptions into a coherent whole
Similarly, analysis is defined as:
· detailed examination of anything complex to understand its nature or to determine its essential features.
· a thorough study: separation of a whole into its component parts
The next step is to test the process based on the mathematical abstraction and generalization method in both Synthesis and Analysis mode.
I will be thinking about applications that are in milieus that are familiar.
· Evolution of electric machine development.
· Volleyball drill development.
The analysis mode is the easier of the two, it entails investigating accepted applications by identifying the parts by going backwards through the process:
· Identifying the results of generalization and identifying the purpose and “logic.”
· Identifying the features of the applications that are left after the abstraction and generalization process.
· Comparing reality as we see them through the different contexts and the applications after the abstraction and generalization.
· Identifying those details that have been abstracted away and determining whether the elimination of those details was necessary and deciding whether more or less details needed to be abstracted away.
The synthesis mode is the most challenging and the most useful application of the process. This is to generate new ideas through the process while adhering to the stated purposes and applying “logic.”
This should be challenging. Stay tuned.
References
Cheng, E. (2016). How to Bake Pi: An Edible Exploration of the Mathematics . Basic Books.
Cheng, E. (2022). The Joy of Abstraction: An Exploration of Math, Category Theory, and Life. Cambridge UK: Cambridge University Press.
Kahneman, D. (2013). Thinking Fast and Slow. New York City: Farrar, Strau, and Giroux.
Kuhn, T. S. (1970). The Structure of Scientific Revolutions. Chicago: University of Chicago Press.
Watts, A. (1957). The Way of Zen. NYC: Random House.